近日,人工智能领域顶级学术刊物《IEEE Transactions on Pattern Analysis and Machine Intelligence》(即IEEE T-PAMI,影响因子17.861)接收了我院“准长聘人才计划” 引进的海外优秀学者曹晓锋副教授的最新研究成果《Distribution Disagreement via Lorentzian Focal Representation》。IEEE T-PAMI,即《IEEE模式分析与机器智能汇刊》,是人工智能、模式识别、计算机视觉及机器学习领域最重要的学术期刊之一,也是当前计算机类别中影响因子最高的期刊,长期位列所有计算机及人工智能相关期刊首位。
概述:
本文证明了在估计误差分歧系数不可行的场景下,如何构造分布差异系数寻找假设空间中的最优解,并使用“洛伦兹焦点” 构造洛伦兹变形空间,进一步缩减欧式变形空间,以获得更严格的标签复杂度的界。本文的动机如下图所示:
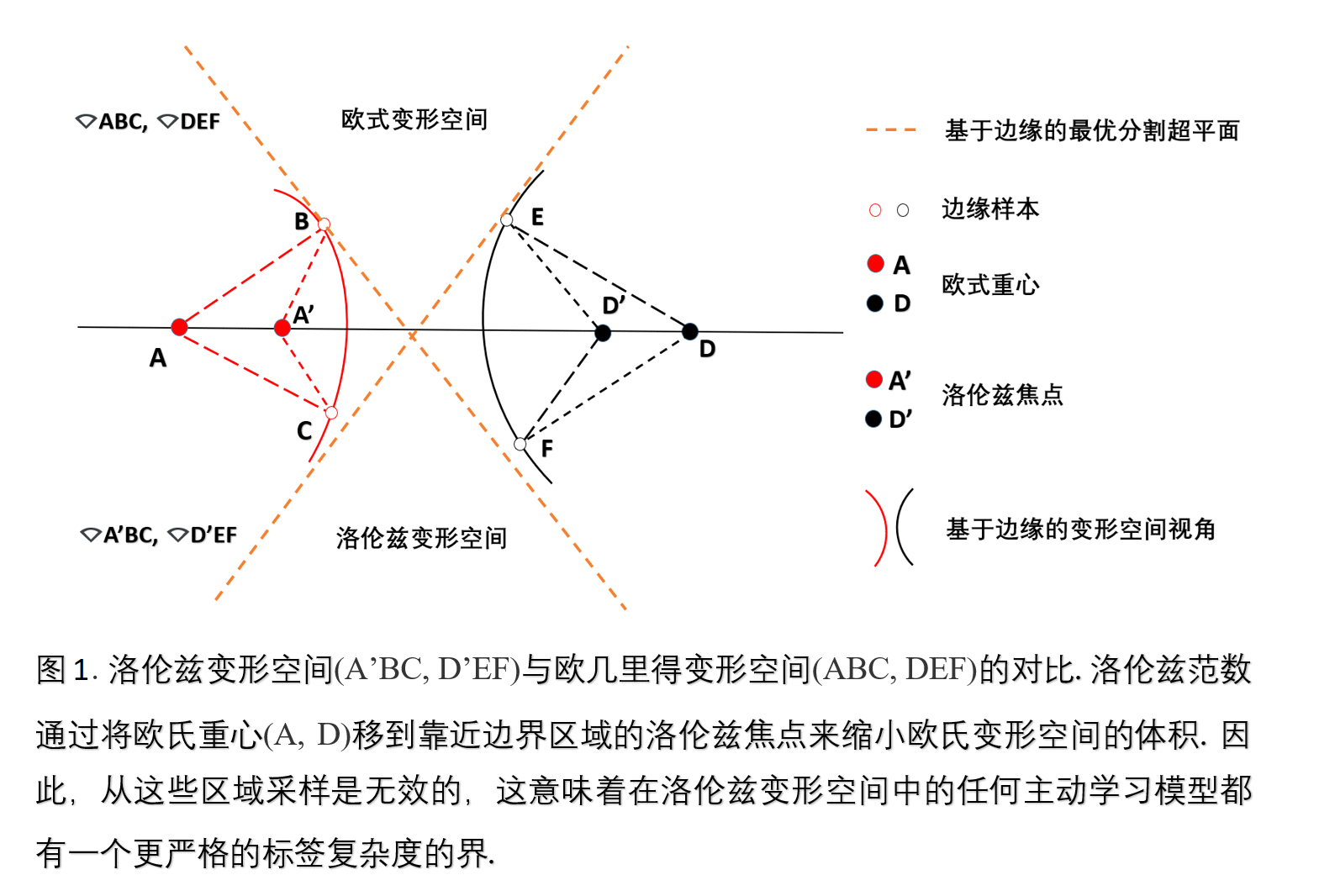
摘要:
误差分歧是学习理论中关于假设更新的重要估计系数和估计量。通常情况下,学习算法优先选择最大化假设更新的潜在未标记数据,进而快速缩减候选假设空间。但是,这一缩减过程严格依赖于初始假设和系数的估计偏置。在应用中,缺乏先验监督(例如,标签不充分,不当的分类器参数)可能会削弱或干扰此更新。此外,使用深度神经网络进行贪婪搜索假设,可能产生不可估量的复杂度。在本文中,一个新的基于分布的(而非基于误差的)分歧系数在标签复杂度上提供了一个更严格的“界”,这进一步保证了它在双曲空间推广的有效性。由洛伦兹平方距离诱导的洛伦焦点,可以呈现出更有效的非欧表征,从而替换典型的欧几里德、核化、和庞加莱质心。实验表明,采用树状分裂的洛伦焦点,显著优于典型的无监督质心表示和误差分歧基线以及基于最新的神经网络监督学习模型,并显著加快了模型的收敛。
该文的前置工作如下:
Cao, X., & Tsang, I. W. (2020). Shattering Distribution for Active Learning. IEEE transactions on neural networks and learning systems.
曹晓锋博士毕业于悉尼科技大学人工智能研究院,将在吉林大学人工智能学院建立 “机器感知课题组”,该研究小组将由国际知名机器学习学者 Ivor Tsang教授参与指导,旨在建立一个具有一流水平的机器学习理论实验室。Ivor Tsang是澳大利亚人工智能研究院研究主任,兼任NeurIPS 2021 Exp Chair, ACML 2021 Co-Chair, ICML 2021 Senior Area Chair,同时也是JMLR、MLJ、T-PAMI、JAIR等机器学习和人工智能旗舰期刊的Editor/Associate Editor。他具有高达18561次的谷歌引用量,H-index指数高达62,曾获得过“国际华人数学家联盟最佳论文奖”,并荣登“AI 2000”澳大利亚最具影响力学者榜单。
欢迎有志攻读博士、硕士研究生学位的同学联系曹博士。邮箱:xiaofeng.cao.uts@gmail.com
